Teorema de Bolzano-Weierstrass
- Teorema de Bolzano-Weierstrass
- Si una función f(x) está definida y es continua en un intervalo cerrado [a,b], entonces f(x) alcanza al menos un máximo (z) y un mínimo (y) absolutos en el intervalo [a,b]. Es decir:
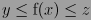 Siendo «x» cualquier valor de la variable perteneciente al dominio de la función.
Demostracion: Primero voy a obtener que el conjunto Im(f) es acotado. La prueba es por el absurdo, supongamos que no es acotada, esto implica que existe una subsucesion xn talque f(xn) tiende a infinito. Pero por estar la sucesion xn acotada (pues esta en I=[a,b]), entonces xn tiende a un valor x que pertenece al I (esto es porque es cerrado). Por lo cual por continuidad f(xn) tiende f(x), pero este es un valor finito, por lo cual llego a un absurdo. La prueba de que esta acotada inferiormente es analoga a la anterior (en la cual solo se probo la acotacion superior). Para probar que hay un maximo vamos a usar que todo conjunto acotado tiene supremo (s)(axioma 14 de los reales) y veremos que existe un xo talque f(xo)=s. Para eso usamos un teorema que dice que siempre hay una sucesion bn de terminos que tienden al supremo , por lo tanto para esa sucesion yo tengo una sucesion de elementos f(an)=bn, tales que en el limite (an tiende a un xo dentro del intervalo) f(xo)=s. Esto prueba que se alcanza un maximo, para probar que alcanza un minimo se usa la parte no demostrada del teorema anterior y el corolario el axioma 14 que dice lo mismo para conjuntos acotados inferiormente.
Siendo «x» cualquier valor de la variable perteneciente al dominio de la función.
Demostracion: Primero voy a obtener que el conjunto Im(f) es acotado. La prueba es por el absurdo, supongamos que no es acotada, esto implica que existe una subsucesion xn talque f(xn) tiende a infinito. Pero por estar la sucesion xn acotada (pues esta en I=[a,b]), entonces xn tiende a un valor x que pertenece al I (esto es porque es cerrado). Por lo cual por continuidad f(xn) tiende f(x), pero este es un valor finito, por lo cual llego a un absurdo. La prueba de que esta acotada inferiormente es analoga a la anterior (en la cual solo se probo la acotacion superior). Para probar que hay un maximo vamos a usar que todo conjunto acotado tiene supremo (s)(axioma 14 de los reales) y veremos que existe un xo talque f(xo)=s. Para eso usamos un teorema que dice que siempre hay una sucesion bn de terminos que tienden al supremo , por lo tanto para esa sucesion yo tengo una sucesion de elementos f(an)=bn, tales que en el limite (an tiende a un xo dentro del intervalo) f(xo)=s. Esto prueba que se alcanza un maximo, para probar que alcanza un minimo se usa la parte no demostrada del teorema anterior y el corolario el axioma 14 que dice lo mismo para conjuntos acotados inferiormente.
Enciclopedia Universal.
2012.
Mira otros diccionarios:
Teorema de Bolzano-Weierstrass — Para el teorema de análisis real, véase Teorema de Weierstrass. En el análisis real, el teorema Bolzano–Weierstrass es un importante teorema que caracteriza los conjuntos secuencialmente compactos. Contenido 1 Enunciado 2 Demostración … Wikipedia Español
Teorema de Weierstrass — El Teorema de Weierstrass es un teorema de análisis real que establece que una función continua en un intervalo cerrado y acotado (de números reales) alcanza sus valores máximo y mínimo en puntos del intervalo. También se puede enunciar en… … Wikipedia Español
Teorema del valor intermedio — Para el teorema de cálculo diferencial, véase Teorema del valor medio. Teorema de los valores intermedios. En análisis real el teorema del valor intermedio (o más correctamente teorema de los valores intermedios, o TVI), es un teorema sobre… … Wikipedia Español
Teorema de Tychonoff — En topología, el teorema de Tychonoff establece que el producto de cualquier colección de espacios topológicos compactos es compacto. El teorema se nombró así por Andrey Nikolayevich Tychonoff, quien lo probó por primera vez en 1930 para… … Wikipedia Español
Karl Weierstrass — Karl Weierstraß Karl Theodor Wilhelm Weierstraß Nacimiento 31 de octubre de 1815 Ostenfelde, Westphalia … Wikipedia Español
Bernard Bolzano — Saltar a navegación, búsqueda Bernard Bolzano Contenido 1 Biografía … Wikipedia Español
Karl Weierstrass — Carlos Teodoro Guillermo Weierstrass (o Weierstraß, en alemán) (31 de octubre de 1815 19 de febrero de 1897) fue un matemático alemán que se suele citar como el «padre del análisis moderno». Nació en Ostenfelde, Westfalia (actualmente Alemania) y … Enciclopedia Universal
Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención … Wikipedia Español
Enunciados matemáticos — Anexo:Enunciados matemáticos Saltar a navegación, búsqueda Contenido 1 Lista de axiomas y postulados 2 Lista de conjeturas e hipótesis 3 Lista de lemas … Wikipedia Español
Anexo:Enunciados matemáticos — Contenido 1 Lista de axiomas y postulados 2 Lista de conjeturas e hipótesis 3 Lista de lemas 4 Lista de teoremas … Wikipedia Español
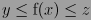 Siendo «x» cualquier valor de la variable perteneciente al dominio de la función.
Demostracion: Primero voy a obtener que el conjunto Im(f) es acotado. La prueba es por el absurdo, supongamos que no es acotada, esto implica que existe una subsucesion xn talque f(xn) tiende a infinito. Pero por estar la sucesion xn acotada (pues esta en I=[a,b]), entonces xn tiende a un valor x que pertenece al I (esto es porque es cerrado). Por lo cual por continuidad f(xn) tiende f(x), pero este es un valor finito, por lo cual llego a un absurdo. La prueba de que esta acotada inferiormente es analoga a la anterior (en la cual solo se probo la acotacion superior). Para probar que hay un maximo vamos a usar que todo conjunto acotado tiene supremo (s)(axioma 14 de los reales) y veremos que existe un xo talque f(xo)=s. Para eso usamos un teorema que dice que siempre hay una sucesion bn de terminos que tienden al supremo , por lo tanto para esa sucesion yo tengo una sucesion de elementos f(an)=bn, tales que en el limite (an tiende a un xo dentro del intervalo) f(xo)=s. Esto prueba que se alcanza un maximo, para probar que alcanza un minimo se usa la parte no demostrada del teorema anterior y el corolario el axioma 14 que dice lo mismo para conjuntos acotados inferiormente.
Siendo «x» cualquier valor de la variable perteneciente al dominio de la función.
Demostracion: Primero voy a obtener que el conjunto Im(f) es acotado. La prueba es por el absurdo, supongamos que no es acotada, esto implica que existe una subsucesion xn talque f(xn) tiende a infinito. Pero por estar la sucesion xn acotada (pues esta en I=[a,b]), entonces xn tiende a un valor x que pertenece al I (esto es porque es cerrado). Por lo cual por continuidad f(xn) tiende f(x), pero este es un valor finito, por lo cual llego a un absurdo. La prueba de que esta acotada inferiormente es analoga a la anterior (en la cual solo se probo la acotacion superior). Para probar que hay un maximo vamos a usar que todo conjunto acotado tiene supremo (s)(axioma 14 de los reales) y veremos que existe un xo talque f(xo)=s. Para eso usamos un teorema que dice que siempre hay una sucesion bn de terminos que tienden al supremo , por lo tanto para esa sucesion yo tengo una sucesion de elementos f(an)=bn, tales que en el limite (an tiende a un xo dentro del intervalo) f(xo)=s. Esto prueba que se alcanza un maximo, para probar que alcanza un minimo se usa la parte no demostrada del teorema anterior y el corolario el axioma 14 que dice lo mismo para conjuntos acotados inferiormente.